工程力学

授课教师 卞培良；刘兆暐

© Pei-Liang Bian.

基本概念及基本原理

力的概念

力是什么？

力是物体间的相互机械作用，这种作用使物体的运动状态发生改变（外效应），或使物体产生变形（内效应）。力使物体运动状态改变的效应称为力的运动效应，使物体产生变形的效应称为力的变形效应。

力对物体作用的效应取决于力的三要素，即力的大小、方向、作用点。 （1.这种矢量又叫什么？定位矢。2.力一定是定位矢吗？为什么？）

度量力的大小通常采用国际单位制（SI）, 力的单位用牛顿（N）或千牛顿（kN）。

注意向量和标量的区分。教材：F\boldsymbol{F},FF, 作业：F→\overrightarrow{F},F‾\overline{F}

静力学基本原理

公理1 平行四边形法则（[力(矢量)的运算法则]）

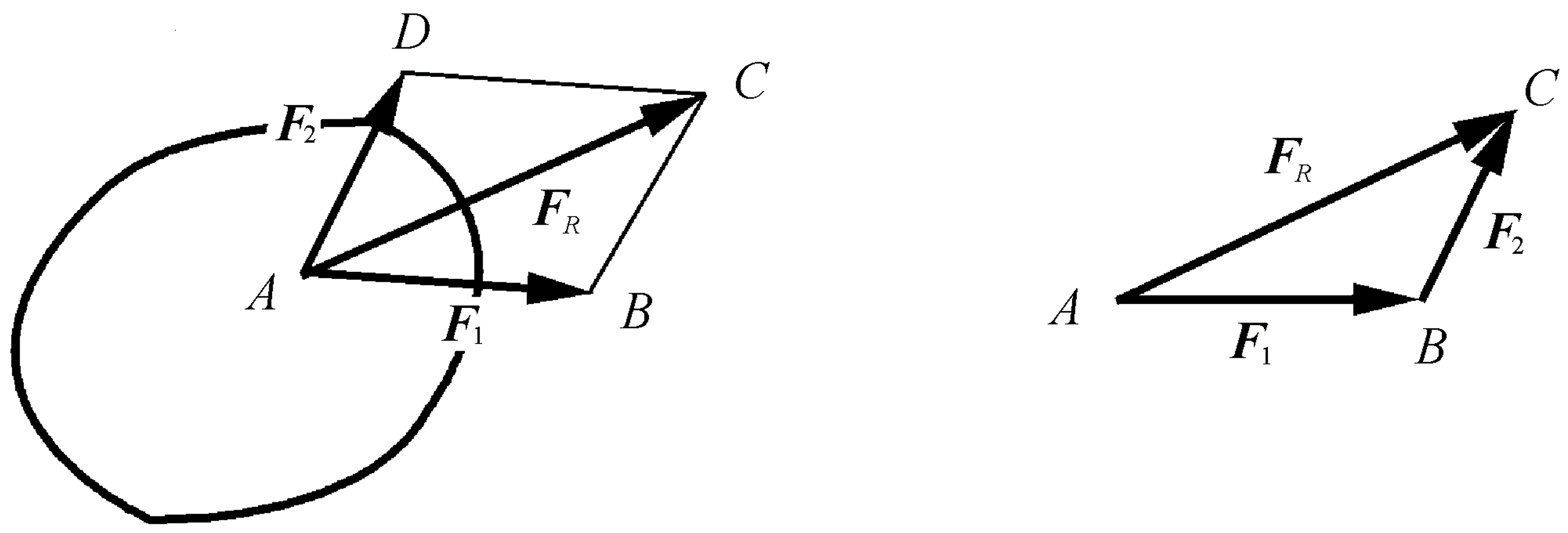
第一个公理是力的平行四边形法则

F→R=F→1+F→2 \overrightarrow{\boldsymbol{F}}_R = \overrightarrow{\boldsymbol{F}}_1+\overrightarrow{\boldsymbol{F}}_2

公理2 二力平衡条件

第二个公理是二力平衡的条件。 作用在刚体上的两个力，使刚体保持平衡的必要和充分条件是：这两个力的大小相等，方向相反，且作用在同一直线上。

使刚体平衡的充分必要条件：

F→1=−F→2 \overrightarrow{\boldsymbol{F}}_1 = -\overrightarrow{\boldsymbol{F}}_2

最简单力系的平衡条件。

公理3 加减平衡力系原理

在任一力系中加上一个平衡力系，或从其中减去一个平衡力系，所得新力系与原力系对于刚体的运动效应相同。

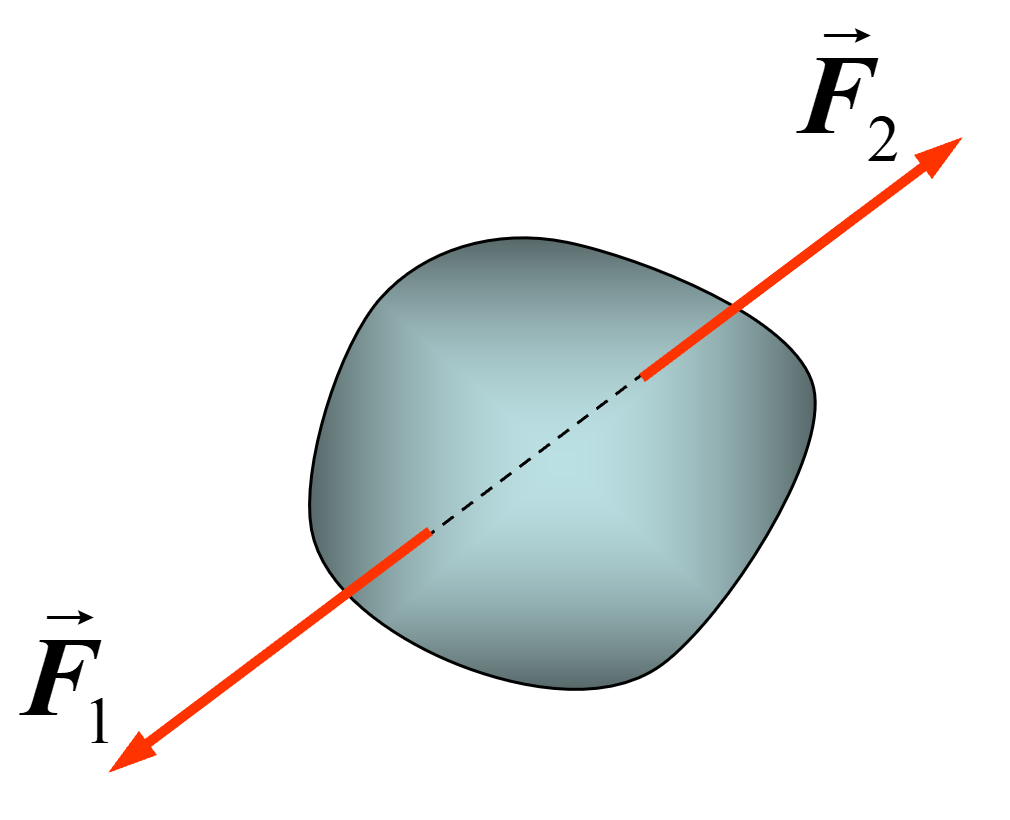
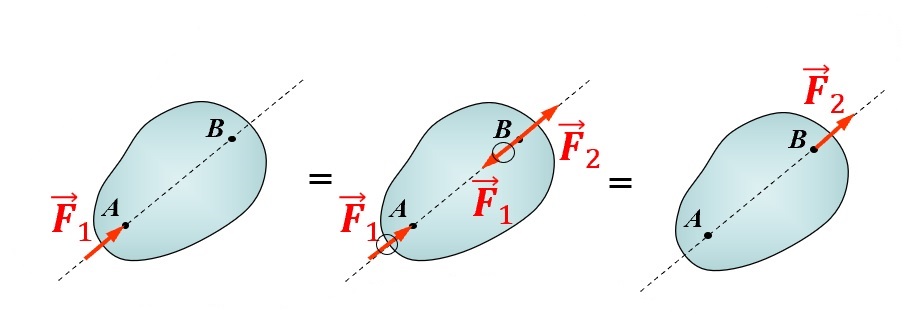
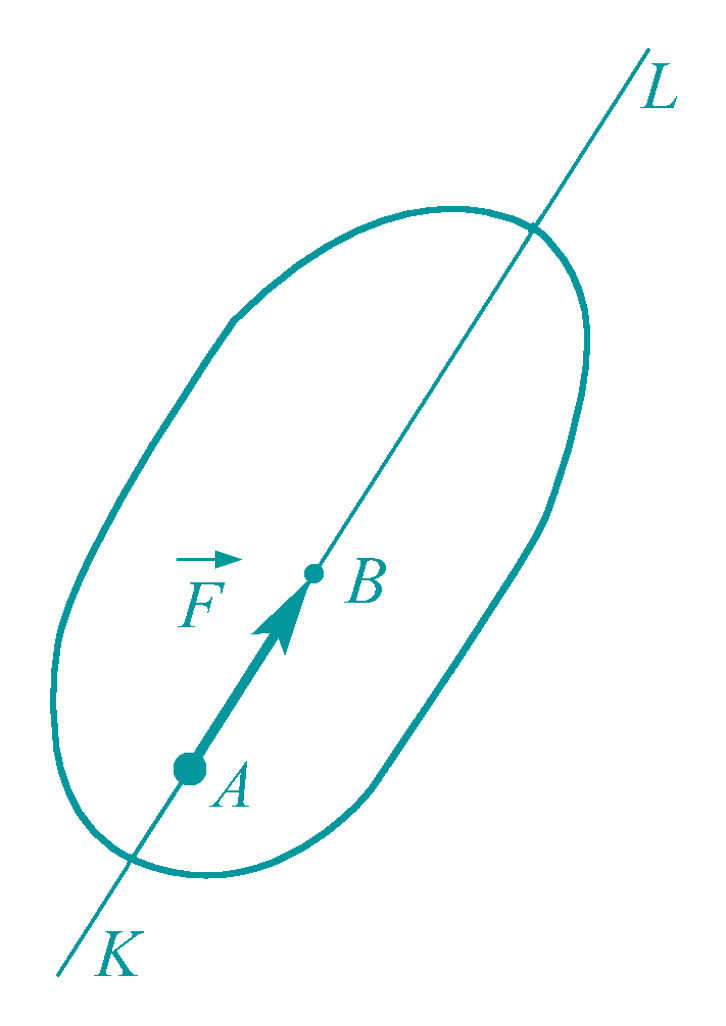
推理： 力的可传性 作用在刚体上的力是滑动矢量，力的三要素为大小、方向和作用线。（注意是同一刚体）

公理4 作用与反作用定律

作用力和反作用力总是同时存在，同时消失，等值、反向、共线，作用在相互作用的两个物体上．

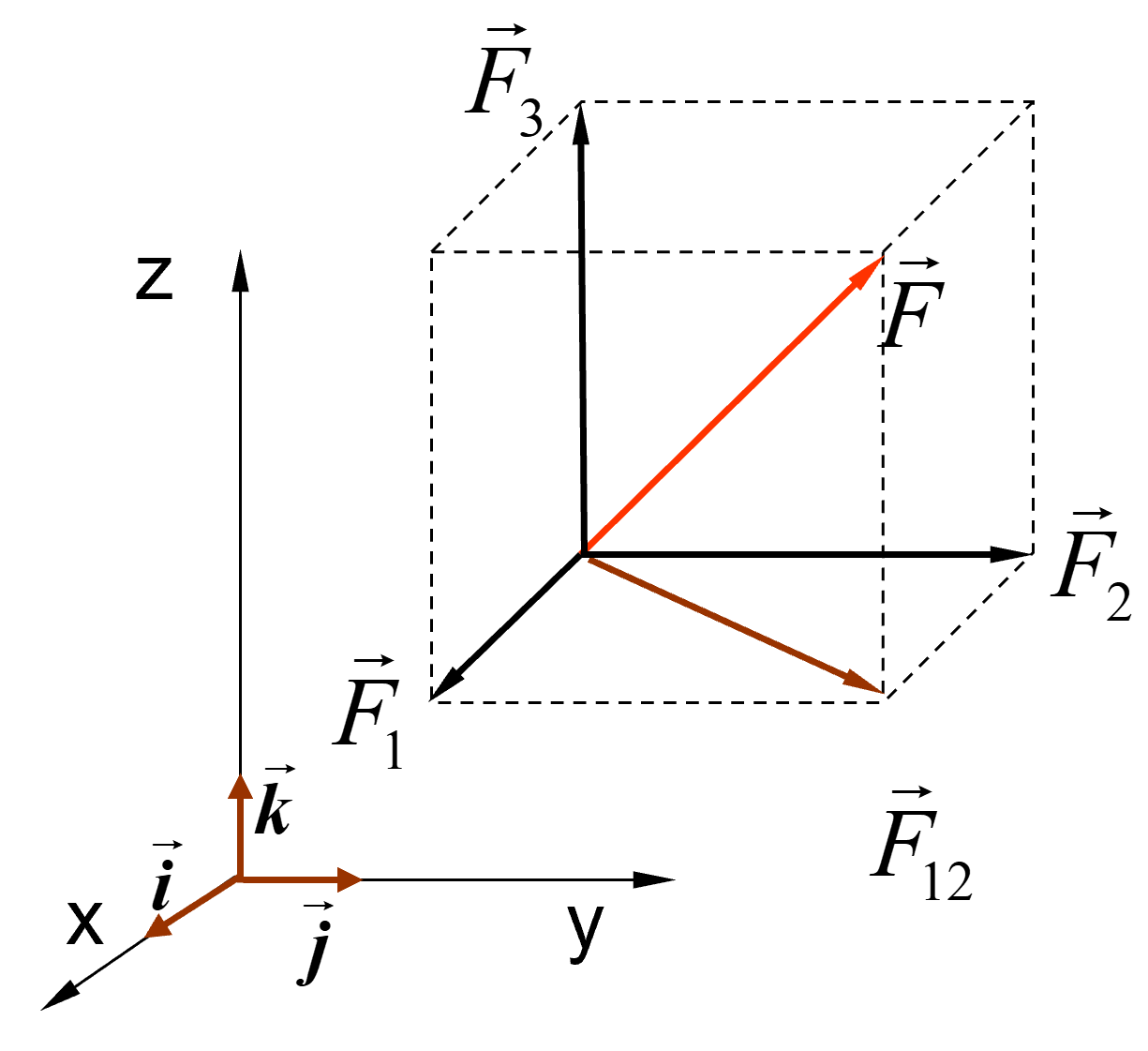
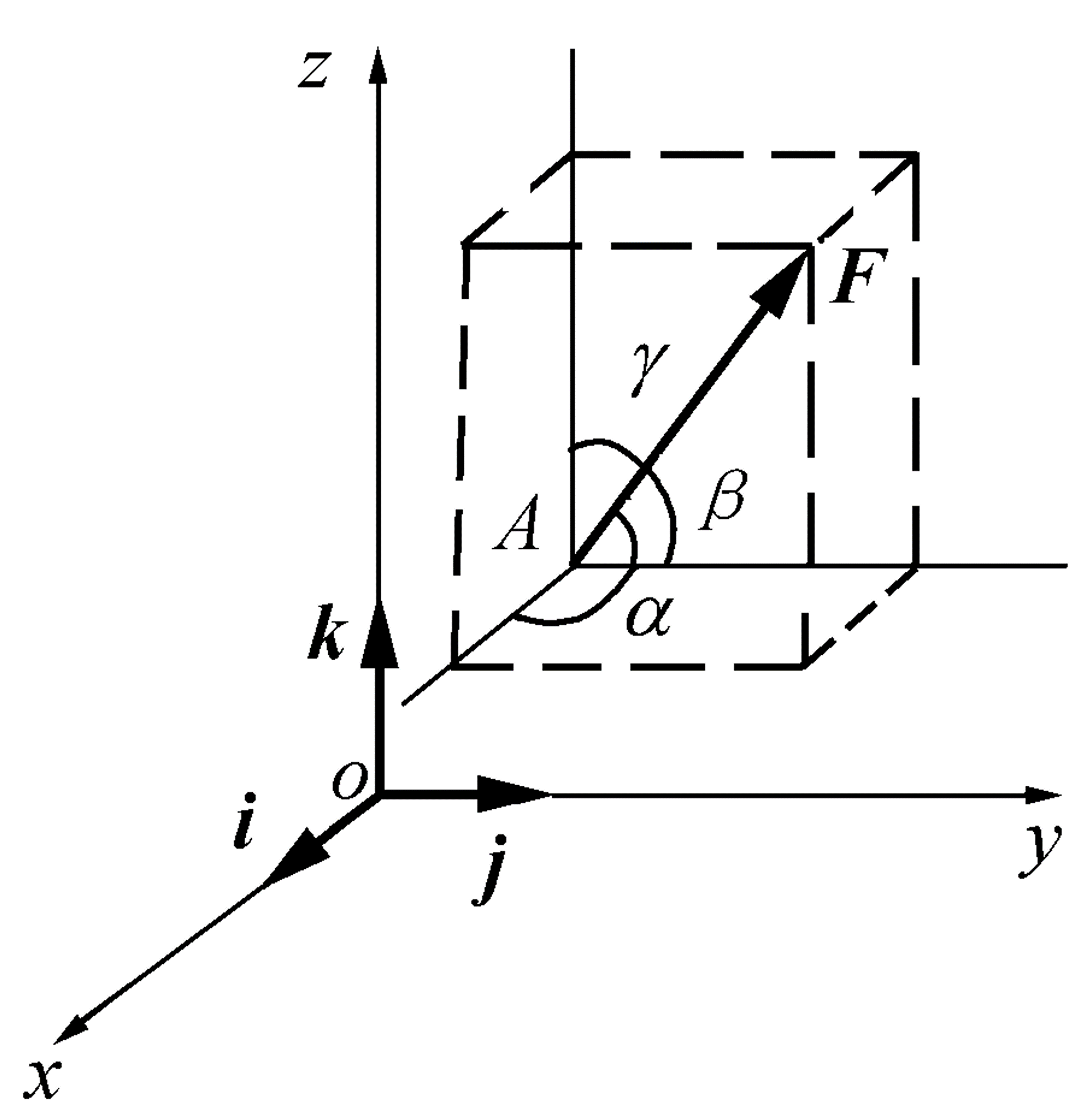
F→=−F′→ \overrightarrow{\boldsymbol{F}} = -\overrightarrow{\boldsymbol{F}^\prime}

力的分解与力的投影

F→=F→12+F→3=F→1+F→2+F→3 \overrightarrow{\boldsymbol{F}}=\overrightarrow{\boldsymbol{F}}_{12}+\overrightarrow{\boldsymbol{F}}_{3}=\overrightarrow{\boldsymbol{F}}_{1}+\overrightarrow{\boldsymbol{F}}_{2}+\overrightarrow{\boldsymbol{F}}_{3}

分解式F→=Fxi→+Fyj→+Fzk→\overrightarrow{\boldsymbol{F}}=F_x \overrightarrow{\boldsymbol{i}}+F_y \overrightarrow{\boldsymbol{j}}+F_z \overrightarrow{\boldsymbol{k}}

投影Fx=F→⋅i→F_x = \overrightarrow{\boldsymbol{F}}\cdot\overrightarrow{\boldsymbol{i}}，Fy=F→⋅j→F_y = \overrightarrow{\boldsymbol{F}}\cdot\overrightarrow{\boldsymbol{j}}，Fz=F→⋅k→F_z = \overrightarrow{\boldsymbol{F}}\cdot\overrightarrow{\boldsymbol{k}}

直接投影法

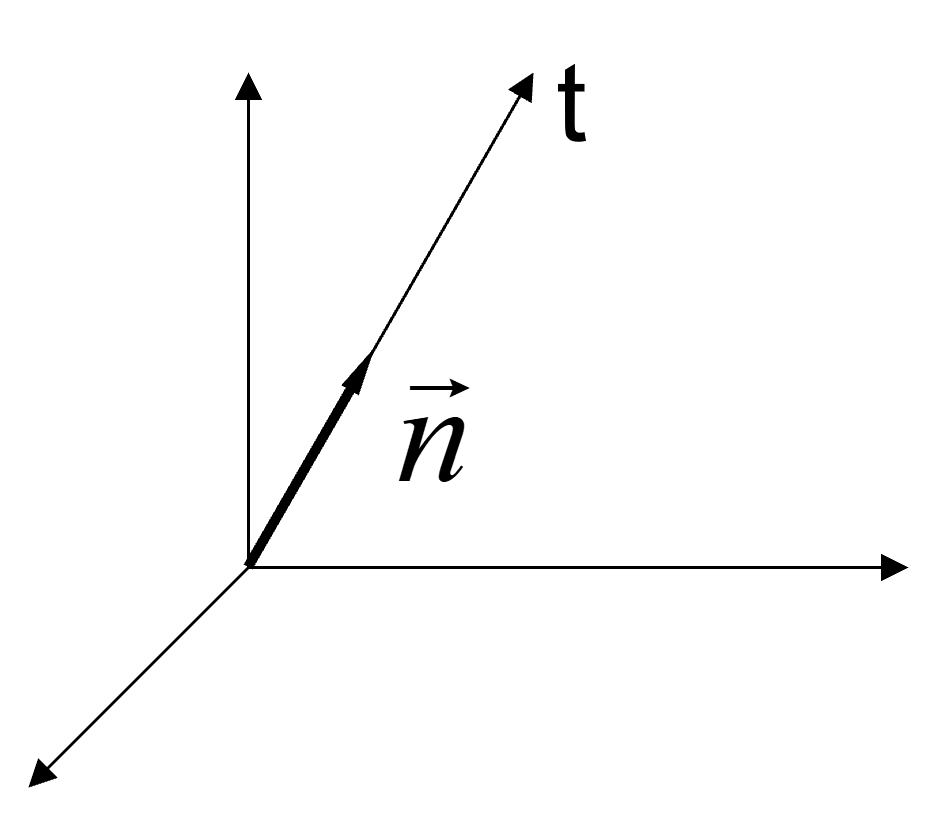
Fx=Fcos⁡α, Fy=Fcos⁡β,Fz=Fcos⁡γ F_x = F \cos\alpha,\ F_y = F \cos\beta, F_z = F \cos\gamma

力在任意轴上的投影

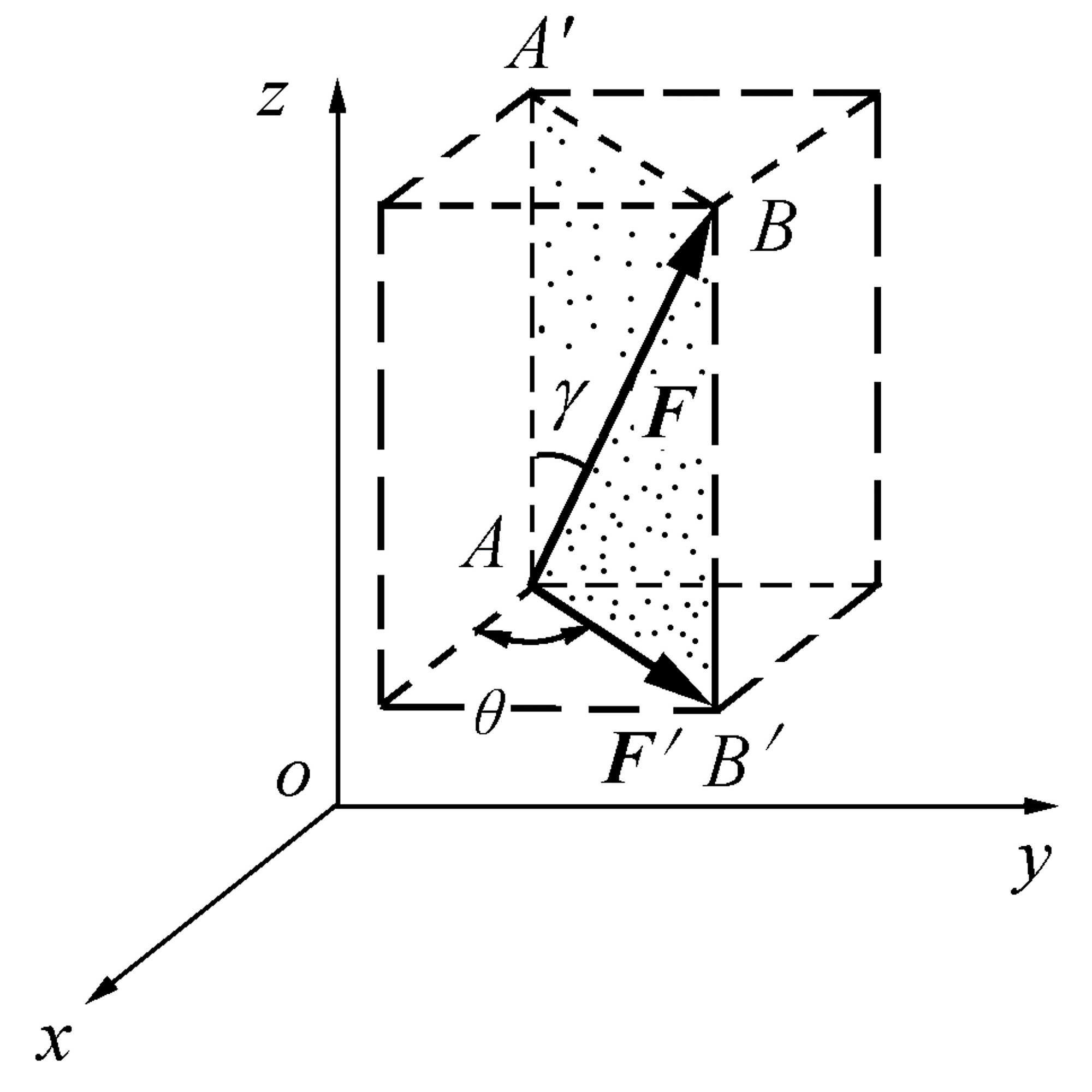
Ft=F→⋅n→=Fxcos⁡α+Fycos⁡β+Fzcos⁡γ F_t = \overrightarrow{F}\cdot\overrightarrow{n} = F_x \cos \alpha + F_y \cos \beta + F_z \cos \gamma F→=Fxi→+Fyj→+Fzj→ \overrightarrow{F} = F_x \overrightarrow{\boldsymbol{i}} + F_y \overrightarrow{\boldsymbol{j}} + F_z \overrightarrow{\boldsymbol{j}} n→=cos⁡αi→+cos⁡βj→+cos⁡γk→ \overrightarrow{n} = \cos \alpha \overrightarrow{\boldsymbol{i}} + \cos \beta \overrightarrow{\boldsymbol{j}} + \cos \gamma \overrightarrow{\boldsymbol{k}}

二次（间接投影法）

在直接知道F→\overrightarrow{\boldsymbol{F}}和各个坐标的夹角，利用上述的直接投影法可以很容易得到F→\overrightarrow{\boldsymbol{F}}在各个坐标轴上的投影。 但是如果仅仅知道F→\overrightarrow{\boldsymbol{F}}和轴与一个平面的夹角φ\varphi和θ\theta，则可以利用二次投影法来进行投影。

二次投影法求投影的解析表达式为：

Fx=F′cos⁡θ=Fsin⁡γcos⁡θFy=F′sin⁡θ=Fsin⁡γsin⁡θFz=Fcos⁡γ \begin{split} F_x & = F^\prime \cos\theta = F \sin \gamma \cos \theta \\ F_y & = F^\prime \sin\theta = F \sin \gamma \sin \theta \\ F_z & = F \cos \gamma \\ \end{split}

若已知力在xx、yy、zz轴上的投影 ，则可求得FF的大小及方向余弦：

F=Fx2+Fy2+Fz2 F = \sqrt{F_x^2+F_y^2+F_z^2} cos⁡α=FxF, cos⁡β=FyF, cos⁡γ=FzF, \cos \alpha = \frac{F_x}{F},\ \cos \beta = \frac{F_y}{F},\ \cos \gamma = \frac{F_z}{F},\

在实际计算投影的过程中，可以根据以力F→\overrightarrow{\boldsymbol{F}}为对角线，各边平行于坐标轴的长方体的各个边长的大小来判断投影的大；再根据力与坐标轴正方向的夹角来判断投影的正负符号。

CC BY-SA 4.0 Pei-Liang Bian. Last modified: August 30, 2022. Website built with Franklin.jl and the Julia programming language.